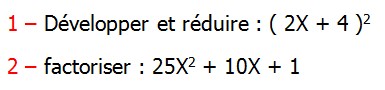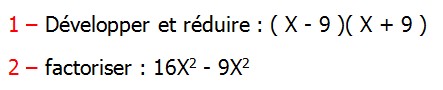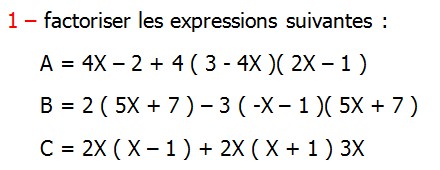MATHÉMATIQUES Exercices Corrigés
Bienvenus
Connexion

Résultats de votre recherche: mathematique

  • Exercices corrigés de maths 3éme Développement Factorisation Identités remarquables

    par lemathematique.com / 21,101 Vues
    EXERCICE DE MATHS 1 Développement Factorisation Identités Remarquables

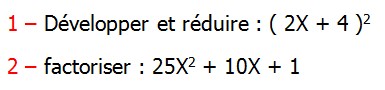
     Exercices corriges de Maths 3ème Cours Mathématique sur les écritures littérales Développement Factorisation Identités Remarquables la double distributivité Développer et réduire : ( 2X + 4 )2 factoriser : 25X2 + 10X + 1

    CORRECTION EXERCICE DE MATHS 1

    EXERCICE DE MATHS 2 Développement Factorisation Identités Remarquables

     Exercices corriges de Maths 3ème Cours Mathématique sur les écritures littérales Développement Factorisation Identités Remarquables la double distributivité Développer et réduire : ( 3X - 3 )2 factoriser : 36X2 - 36X + 9

    CORRECTION EXERCICE DE MATHS 2

    EXERCICE DE MATHS 3 Développement Factorisation Identités Remarquables

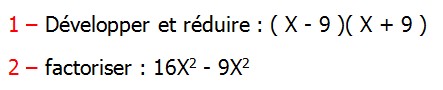
     Exercices corriges de Maths 3ème Cours Mathématique sur les écritures littérales Développement Factorisation Identités Remarquables la double distributivité Développer et réduire : ( X - 9 )( X + 9 ) factoriser : 16X2 - 9X2

    CORRECTION EXERCICE DE MATHS 3

    EXERCICE DE MATHS 4 Développement Factorisation Identités Remarquables

     Exercices corriges de Maths 3ème Cours Mathématique sur les écritures littérales Développement Factorisation Identités Remarquables la double distributivité factoriser les expressions suivantes 3X + 6 ; -X + 2X2 ; 5X2 + 10X - 25XY

    CORRECTION EXERCICE DE MATHS 4

    EXERCICE DE MATHS 5 Développement Factorisation Identités Remarquables

     Exercices corriges de Maths 3ème Cours Mathématique sur les écritures littérales Développement Factorisation Identités Remarquables la double distributivité Développer les expressions suivantes -5X ( 2X- 1/5 X+ 2/5 Y-3 ) ; ( -3X – 3 )( 6 - 5X )

    CORRECTION EXERCICE DE MATHS 5

    EXERCICE DE MATHS 6 Développement Factorisation Identités Remarquables

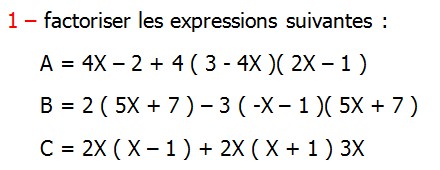
     Exercices corriges de Maths 3ème Cours Mathématique sur les écritures littérales Développement Factorisation Identités Remarquables la double distributivité factoriser les expressions suivantes A = 4X – 2 + 4 ( 3 - 4X )( 2X – 1 ) B = 2 ( 5X + 7 ) – 3 ( -X – 1 )( 5X + 7 ) C = 2X ( X – 1 ) + 2X ( X + 1 ) 3X

    CORRECTION EXERCICE DE MATHS 6

    EXERCICE DE MATHS 7 Développement Factorisation Identités Remarquables

     Exercices corriges de Maths 3ème Cours Mathématique sur les écritures littérales Développement Factorisation Identités Remarquables la double distributivité A = ( 3X - 2 )2 - ( 3X - 2 )( X + 3 ) Développer et réduire : A factoriser : A

    CORRECTION EXERCICE DE MATHS 7

    EXERCICE DE MATHS 8 Développement Factorisation Identités Remarquables
    1 - Développer et réduire les expressions suivants :
    A = 2 ( Χ + 3 ) B = 5 ( - Χ - 2 ) C = 7 ( 7 - Χ )
    D = - 3 ( Χ - 10 ) E = - 2 ( - Χ + 6 ) F = 4 ( 3Χ + 2 )
    G  = 11 ( - 11Χ - 10 ) H = 6 ( 8 - 15Χ )
    		I = - 8 ( 3Χ + 4 )

    J = - (  2Χ + 5 )

    		 K = - Χ ( Χ + 2 )
    		L  = 3Χ ( - 2Χ - 5 )

    CORRECTION EXERCICE DE MATHS 8

    A = 2 ( Χ + 3 ) B = 5 ( - Χ - 2 ) C = 7 ( 7 - Χ )
    A = 2 × Χ + 2 × 3
    		B = 5 × ( - Χ ) + 5 × ( - 2 ) C = 7 × 7 + 7 × (- Χ )
    A = 2Χ + 6 B = - 5 Χ - 10
    		C = 49 - 7Χ
     
    D = - 3 ( Χ - 10 )  E = - 2 ( - Χ + 6 )  F = 4 ( 3Χ + 2 )
    D = - 3 × Χ + ( - 3 ) × ( - 10 ) 
    		E = - 2 × (- Χ ) + ( - 2 ) × 6
    		 F = 4 × 3Χ + 4 × 2
    D = - 3Χ + 30  E = 2Χ - 12
    		 F = 12Χ + 8
     
    G  = 11 ( - 11Χ - 10 ) H = 6 ( 8 - 15Χ )  I = - 8 ( 3Χ + 4 ) 
    G  = 11 × (- 11Χ) + 11 × (- 10) H = 6 × 8 - 6 × 15Χ   I = ( - 8 ) × 3Χ + ( -8 ) × 4 
    G  = -121Χ - 110   H = 48 - 90Χ   I = - 24Χ - 32 
     
     J = - (  2Χ + 5 ) K = - Χ ( Χ + 2 )  L  = 3Χ ( - 2Χ - 5 )
     J = -  2Χ - 5 
    		 K = ( - Χ ) × Χ + ( - Χ ) × 2  L  = 3Χ × (- 2Χ ) + 3Χ × (- 5)
      K = - Χ2   2Χ  L  = - 6Χ2 - 15Χ  
    EXERCICE DE MATHS 9 Développement Factorisation Identités Remarquables
    1 - Développer et réduire les expressions suivants :
    A = ( Χ + 3 )( 5 + Χ )
    		 B = ( - Χ - 2 )( - Χ - 2 )
    		 C = ( - 3Χ + 1 )( Χ - 4 )
    D = ( - 9 - Χ )( Χ + 6 )
    		 E = ( 2Χ + 11 )( 3Χ + 2 )
    		 F = ( 6Χ - 9 )( - 2Χ + 8 )
    G = ( - Υ - Χ )( - 7 + Χ )
    		 H = ( - Χ - 8Υ )( - 4Χ + 6 )
    		 I = ( - 7Χ - 7 )( - 7Χ - 7 )
    J = ( - 4 + 5Χ )( - 5Χ - 3 )
    		 K= ( - 2Υ - Χ )( - 6Χ - 8 ) L = ( - Υ - 7Χ ) ( - 2Χ - 5 )

    CORRECTION EXERCICE DE MATHS 9

    A = ( Χ + 3 )( 5 + Χ ) B = ( - Χ - 2 )( - Χ - 2 )
    A = Χ × 5 + Χ × Χ + 3 × 5 + 3 × Χ B = -Χ ×(-Χ)+(-Χ)×(-2)+(-2)×(-Χ )+(-2)×(-2)
    A = 5Χ + Χ2 + 15 + 3Χ B = Χ2 + 2Χ + 2Χ + 4 
    A = 8Χ + 15 + Χ2  B = Χ2 + 4Χ + 4
      B  =  ( Χ + 2 )2
       
    C = ( - 3Χ + 1 )( Χ - 4 ) D = ( - 9 - Χ )( Χ + 6 )
    C = -3Χ × Χ+(-3Χ )×(-4 )+1× Χ +1×(-4 ) D = - 9 × Χ +(-9)×6 + (-Χ) × Χ +(-Χ)× 6
    C = - 3Χ2 + 12Χ + Χ -  4 D = - 9Χ + ( - 54 ) + ( -Χ2 ) + ( - 6Χ ) 
    C = - 3Χ2  + 13Χ - 4 D = - Χ2 - 15Χ  - 54
       
    E = ( 2Χ + 11 )( 3Χ + 2 ) F = ( 6Χ - 9 )( - 2Χ + 8 )
    E = 2Χ × 3Χ + 2Χ × 2 + 11 × 3Χ + 11 × 2 F = 6Χ ×(-2Χ)+6Χ×8+(-9)×(-2Χ)+(-9)×8
    E = 6Χ2 + 4Χ + 33Χ + 13 F = - 12Χ2 + 48Χ + 18Χ + ( - 72 )
    E = 6Χ2 + 37Χ + 13 F = - 12Χ2 + 66Χ - 72
       
    G = ( - Υ - Χ )( - 7 + Χ ) H = ( - Χ - 8Υ )( - 4Χ + 6 )
    G = -Υ ×(-7)+(-Υ)× Χ+(-Χ)×(-7)+(- Χ)× Χ H = -Χ ×(-4Χ)+(-Χ)×6+(-8Υ)×(-4Χ)+(-8Υ)×6
    G = 7Υ + ( - ΧΥ ) + 7Χ + ( - Χ2 ) H = 4Χ2 + (-6Χ) + 32ΧΥ + (- 48Υ) 
    G = - Χ2   ΧΥ  + 7Χ + 7Υ 
    		 H = 4Χ2 + 32ΧΥ - 6Χ - 48Υ 
       
    I = ( - 7Χ - 7 )( - 7Χ - 7 ) J = ( - 4 + 5Χ )( - 5Χ - 3 )
    I = -7Χ×(-7Χ)+(-7Χ)×(-7)+(-7)×(-7Χ)+(-7)× (-7) J = -4×(-5Χ)+(-4)×(-3)+5Χ×(-5Χ)+5Χ×(-3)
    I = 49Χ2 + 49Χ + 49Χ + 49 J = 20Χ + 12 + (- 25Χ2) + ( - 15Χ ) 
    I = 49Χ2 + 98Χ + 49 J = - 25Χ2 + 5Χ + 12 
    I = ( 7Χ )2 + 2 × 7Χ × 7 + ( 7 )2   
    I = ( 7Χ + 7 )2  
       
    K = ( - 2Υ - Χ )( - 6Χ - 8 ) L = ( - Υ - 7Χ ) ( - 2Χ - 5 )
    K = -2Υ×(-6Χ)+(-2Υ)×(-8)+(-Χ)×(-6Χ)+(-Χ)× (-8) L = -Υ×(-2Χ)+(-Υ)×(-5)+(-7Χ)×(- 2Χ)+(-7Χ)×(-5)
    K = 12ΧΥ + 16Υ + 6Χ2 + 8Χ
    		 L = 2ΥΧ + 5Υ + 14Χ2 + 35Χ
    K = 6Χ2 + 12ΧΥ + 16Υ +  8Χ
    		 L = 14Χ2 + 2ΥΧ + 5Υ +  35Χ
    EXERCICE DE MATHS 10 Développement Factorisation Identités Remarquables
    1 - Développer et réduire les expressions suivantes :
    A =  ( Χ + 3 )2 B = ( - Χ - 2 )2 C = ( 7 - Χ )2
    D = ( 3Χ + 10 )2 E = ( - 2Χ + 6 )2 F = ( 3Χ - 5 )2
    G  = (1,1Χ + 0,5 )2 H = ( 5Χ + 4 )(4 - 5Χ )
    		I = ( 2Χ + 0.5 )( 2Χ + 0.5 )

    J = ( - 3Χ + 9 )( 3Χ + 9 )

    		 K = ( Υ + 8 )( Υ + 8 )
    		 L  =  ( 2Υ + 5 )( - 2Υ + 5 )

    CORRECTION EXERCICE DE MATHS 10

    A =  ( Χ + 3 )2     La forme de ( a + b )2 = a2 + 2ab + b2    tel que     a = Χ et b = 3    alors :
    A =  Χ2 + 2 × 3 × Χ + 32
    A =  Χ2 + 6Χ + 9
     
    B = ( - Χ - 2 )2     La forme de ( a - b )2 = a2 - 2ab + b2     tel que      a = - Χ et b = 2    alors :
    B = ( - Χ )2 - 2 × ( - Χ ) × 2 +  22
    B =  Χ2 + 4Χ + 4
     
    C = ( 7 - Χ )2        La forme de ( a - b )2 = a2 - 2ab + b2     tel que      a = 7 et b = Χ    alors :
    C = 72 - 2 × 7 × Χ +  Χ2
    C = Χ2 - 14Χ + 49
     
    D = ( 3Χ + 10 )2    La forme de ( a + b )2 = a2 + 2ab + b2    tel que  a = 3Χ et b = 10   alors :
    D = ( 3Χ)2 + 2 × 3Χ × 10 + 102
    D = 9Χ2 + 60Χ + 100
     
    E = ( - 2Χ + 6 )2     
    E = ( 6 - 2Χ  )2     La forme de ( a - b )2 = a2 - 2ab + b2     tel que      a = 6 et b = 2Χ    alors :
    E = 62 - 2 × 6 × 2Χ + ( 2Χ )2
    E = 36 - 24Χ + 4Χ2
     
    F = ( 3Χ - 5 )2      La forme de ( a - b )2 = a2 - 2ab + b2     tel que   a = 3Χ et b = 5  alors :
    F = ( 3Χ)2 - 2 × 3Χ × 5 + 52
    F = 9Χ2 - 30Χ + 25
     
    G  = (1,1Χ + 0,5)2  La forme de (a + b)2 = a2 + 2ab + b2  tel que a = 1,1Χ et b = 0,5 alors :
    G  = ( 1,1Χ )2 + 2 × 1,1Χ × 0,5 + ( 0,5 )2 
    G  = 1,21Χ2 + 1,1Χ + 0,25
     
    H = ( 5Χ + 4 )(4 - 5Χ ) La forme de ( a - b )( a + b ) = a2 - b2  tel que  a = 4 et b = 5Χ  alors :
    H = 42 - ( 5Χ )2
    H = 16 - 25Χ2
     
    I = (2Χ+0.5)(2Χ+0.5) La forme de (a+b)(a+b) = a2 + b2 tel que a = 2Χ et b = 0.5 alors :
    I = ( 2Χ)2 + 0.52
    I = 4Χ2 + 0.25
     
    J = ( - 3Χ + 9 )( 3Χ + 9 )  
    J = ( 9 - 3Χ )( 9 + 3Χ ) La forme de ( a - b )( a + b ) = a2 -  b2  tel que a = 9 et b = 3Χ alors :
    J = 92 - ( 3Χ )2
    J = 81 - 9Χ2
     
    K = ( Υ + 8 )( Υ + 8 ) La forme de ( a + b )( a + b ) = a2 + b2  tel que  a = Υ et b = 8  alors :
    K = Υ2 + 82
    K = Υ2 + 64
     
    L  =  ( 2Υ + 5 )( - 2Υ + 5 )
    L  =  ( 5 - 2Υ )( 5 + 2Υ ) La forme de (a - b )( a + b) = a2 - b2 tel que  a = 5 et b = 2Υ alors :
    L  =  52 - ( 2Υ )2
    L  =  25 - 4Υ2
    EXERCICE DE MATHS 11 Développement Factorisation Identités Remarquables
    1 - Factoriser les expressions suivantes :
    A =  5Χ + 45 I = 36Χ2 - ¼
    B = - 6Χ2 - 2Χ J = ( 2Χ - 2 )2 - ( 2Χ - 1 )2
    C = 15Χ - 20 K =( - Χ - 4 )2 - ( Χ - 5 )2
    D = - 3Χ3 +  12Χ L = 9Χ2 + 12Χ + 4 - ( Χ - 1 )( 3Χ +2 )
    E = 81Χ2 - 36 M = ( 15Χ2 + 5 )( Χ - 1 ) + ( Χ - 1 )( - 5 )
    F = Χ2 - Χ + 0.25
    		 N = - 13( Χ + 4 ) - 7Υ( Χ + 4 ) 
    G = ( Χ - 1 )2 + 0.25 
    		 O = 8Χ( - 2Υ + 11 ) + 2Υ - 11
    H = 64 - ( - Χ + 8 )2 
    		 P = - 19Υ( 7Χ - 8 ) + ( Υ - 1 )( - 7Χ + 8 )

    CORRECTION EXERCICE DE MATHS 11

     A =  5Χ + 45    B = - 6Χ2 - 2Χ  
        = 5 × Χ + 5 × 9      = - 2Χ × 3Χ  - 2Χ × 1
        = 5( Χ + 9 )      = - 2Χ( 3Χ + 1 )
       
     C = 15Χ - 20   D = - 3Χ3 +  12Χ  
        = 5 × 3Χ + 5 × 4       = - 3Χ × Χ2 + ( - 3Χ ) × ( - 4 )
        = 5( 3Χ - 4 )      = - 3Χ( Χ2 - 4 )
       
     E = 81Χ2 - 36    F = Χ2 - Χ + 0.25  
        = ( 9Χ )2  - 62     =  (Χ )2 - 2 × 0.5 × Χ + ( 0.5 )2
        = ( 9Χ -  6 )( 9Χ + 6 )     = ( Χ - 0,5 )2
       
     G = ( Χ - 1 )2 + 0.25     H = 64 - (- Χ + 8 )2  
         = ( Χ - 1 )2 + ( 0.5 )2      = 82 - (- Χ + 8 )2
         = ( Χ - 1 + 0,5 )( Χ - 1 + 0,5 )      = [ 8 - ( - Χ + 8 )][ 8 + ( - Χ + 8 )] 
         = ( Χ - 0,5 )( Χ - 0,5 )      = ( 8 + Χ - 8 )( 8 - Χ + 8 ) = Χ( 16 - Χ )
         = ( Χ - 0,5 )2      = Χ( 16 - Χ )
       
     I = 36Χ2 - ¼    J = ( 2Χ - 2 )2 - ( 2Χ - 1 )2 
       = ( 6Χ )2 - ( ½ )2     = [( 2Χ - 2 ) - ( 2Χ - 1 )][( 2Χ - 2 ) + ( 2Χ - 1 )]
       = ( 6Χ - ½ )( 6Χ + ½ )     = ( 2Χ - 2 - 2Χ + 1 )( 2Χ - 2 + 2Χ - 1 ) 
          = ( - 1 )( 4Χ - 3 ) = 3 - 4Χ
       
     K = ( - Χ - 4 )2 - ( Χ - 5 )2   L = 9Χ2 + 12Χ + 4 - ( Χ - 1 )( 3Χ + 2 ) 
        = [( - Χ - 4 ) - ( Χ - 5 )][( - Χ - 4 ) + ( Χ - 5 )]     = ( 3Χ )2 + 2 × 2 × 3Χ + 22 - ( Χ - 1 )( 3Χ + 2 )
        = ( - Χ - 4 - Χ + 5 )( - Χ - 4 + Χ - 5 )      = ( 3Χ + 2 )2 - ( Χ - 1 )( 3Χ + 2 ) 
        = ( - 2Χ + 1 )( - 9 ) = 9( 2Χ - 1 )     = (3Χ + 2)[(3Χ + 2) - (Χ - 1)]= (3Χ + 2)(2Χ + 3) 
       
     M = ( 15Χ2 + 5 )( Χ - 1 ) + ( Χ - 1 )( - 5 )   N = - 13( Χ + 4 ) - 7Υ( Χ + 4 ) 
         = ( Χ - 1 )( 15Χ2 + 5 - 5 )       = ( Χ + 4 )( - 13 - 7Υ )
         = 15Χ2 × ( Χ - 1 )   
         = ( Χ - 1 )15Χ2  
       
     O = 8Χ( - 2Υ + 11 ) + 2Υ - 11   P = - 19Υ( 7Χ - 8 ) + ( Υ - 1 )( - 7Χ + 8 ) 
         = - 8Χ( 2Υ - 11 ) + ( 2Υ - 11 )      = 19Υ( - 7Χ + 8 ) + ( Υ - 1 )( - 7Χ + 8 )
         = ( 2Υ - 11 )( 1 - 8Χ )     = ( - 7Χ + 8 )( 19Υ + Υ - 1 ) 
          = ( - 7Χ + 8 )( 20Υ - 1 )

    Une explication complète Ecritures Littérales Développement Factorisation Identités remarquables avec des exercices appliqués et bien corriges en mathématique pour le niveau troisième

    FICHES DE MATHÉMATIQUES POUR LE NIVEAU TROISIÈME
    Continuer »

Sites Amis Cours Exercices de Maths :

♦ MATHEMATIQUE FRANCAIS ET ARABE 

♦ MATHEMATIQUE EN ARABE
RSS