Exercices corrigés de maths 4éme Nombres relatifs en écriture décimale
| EXERCICE DE MATHS 1 | Nombres relatifs en écriture décimale |
CORRECTION EXERCICE DE MATHS 1
| EXERCICE DE MATHS 2 | Nombres relatifs en écriture décimale |
CORRECTION EXERCICE DE MATHS 2
| EXERCICE DE MATHS 3 | Nombres relatifs en écriture décimale |
CORRECTION EXERCICE DE MATHS 3
| EXERCICE DE MATHS 4 | Nombres relatifs en écriture décimale |
CORRECTION EXERCICE DE MATHS 4
| EXERCICE DE MATHS 5 | Nombres relatifs en écriture décimale |
CORRECTION EXERCICE DE MATHS 5
| EXERCICE DE MATHS 6 | Nombres relatifs en écriture décimale |
CORRECTION EXERCICE DE MATHS 6
| EXERCICE DE MATHS 7 | Nombres relatifs en écriture décimale |
CORRECTION EXERCICE DE MATHS 7
| EXERCICE DE MATHS 8 | Nombres relatifs en écriture décimale |
|
1 - Quel est le résultat de : ( - 5 ) + 12 + ( - 8 ) A = 19 ; B = - 1 ; C = - 2 ; D = 0 ; E = 1 |
CORRECTION EXERCICE DE MATHS 8
B = - 1
| EXERCICE DE MATHS 9 | Nombres relatifs en écriture décimale |
|
1 - Quel est le résultat de : - ½ A = 0,5 ; B = - 2 ; C = - 1 ; D = - 0,5 |
CORRECTION EXERCICE DE MATHS 9
D = - 0,5
| EXERCICE DE MATHS 10 | Nombres relatifs en écriture décimale |
|
: Sans faire les calculs de ces opérations A = ( - 5 ) × 4,2 ; B = ( - 2 ) × ( - 3,8 ) C = ( - 2 ) × ( 3,8 ) ; D = ( - 5 ) × ( - 4,2 ) 1 - Lequel de ces opérations donne le plus grand résultat ? 2 - Lequel de ces opérations donne le plus petite résultat ? |
CORRECTION EXERCICE DE MATHS 10
1 - D = ( - 5 ) × ( - 4,2 )
2 - A = ( - 5 ) × 4,2
| EXERCICE DE MATHS 11 | Nombres relatifs en écriture décimale |
|
1 - Un seul résultat de ces calculs est négatif. LEQUEL ? A = ( - 3,2 ) × 4,2 × ( - 12 ) × 4 B = ( - 10 ) × ( - 45 ) × ( - 0,5 ) × ( - 8 ) C = ( - 5 ) × 1,2 × ( - 11 ) × ( - 0,4 ) D = ( - 13,1 ) × 6 × ( - 6 ) × 25,4 |
CORRECTION EXERCICE DE MATHS 11
C = ( - 5 ) × 1,2 × ( - 11 ) × ( - 0,4 )
| EXERCICE DE MATHS 12 | Nombres relatifs en écriture décimale |
|
1 - Un seul résultat de ces calculs est positif. LEQUEL ? A = ( - 51 ) × 40 × ( - 3,1 ) × ( - 7 ) B = ( - 5 ) × ( - 2 ) × ( - 1,95 ) × ( - 88 ) C = ( - 5 ) × 1.2 × 35 × 0,8 D = ( - 3,9 ) × ( - 6 ) × ( - 19 ) |
CORRECTION EXERCICE DE MATHS 12
B = ( - 5 ) × ( - 2 ) × ( - 1,95 ) × ( - 88 )
| EXERCICE DE MATHS 13 | Nombres relatifs en écriture décimale |
1 - Calculer les opérations suivantes :
|
A = 35 × 94 ; B = 72 × ( -5 )3 ; |
C = ( -1 )1008 D = ( -1 )5009 |
CORRECTION EXERCICE DE MATHS 13
| A = 35 × 94 | B = 72 × ( -5 )3 |
| A = 3 × 3 × 3 × 3 × 3 × 9 × 9 × 9 × 9 | B = 7 × 7 × ( -5 ) × ( -5 ) × ( -5 ) |
| A = 243 × 6 561 | B = 49 × ( -125 ) |
| A = 1 594 323 | B = - 6 125 |
| C = ( -1 )1008 | D = ( -1 )5009 |
| 1008 est un nombre pair | 5009 est un nombre impair |
| donc le résultat positif | donc le résultat négatif |
| C = 1 | D = - 1 |
| EXERCICE DE MATHS 14 | Nombres relatifs en écriture décimale |
|
1 - Calculer les expressions suivantes : |
|
A = - 12 + 4 - ( - 3,6 - 23 ) + ( - 102 ) B = 39 + 18 + ( - 15 + 2 ) - 52 - 5,36 |
CORRECTION EXERCICE DE MATHS 14
| A = - 12 + 4 - ( - 3,6 - 23 ) + ( - 102 ) | B = 39 + 18 + ( - 15 + 2 ) - 52 - 5.36 |
| A = - 8 - ( - 26,6 ) + ( - 102 ) | B = 57 + ( - 13 ) - 57,36 |
| A = - 8 + 26,6 - 102 | B = 57 - 13 - 57,36 |
| A = 18,6 - 102 | B = 44 - 57,36 |
| A = - 83,4 | B = - 13,36 |
| EXERCICE DE MATHS 15 | Nombres relatifs en écriture décimale |
| A = ( 3Χ - 4 ) ( - 6 + Χ ) |
| 1 - Calculer la valeur de A dans les cas suivantes : |
| a) Χ = - 2 ; b) Χ = 7 ; c) Χ = - 1,5 ; d) Χ = - 11 |
CORRECTION EXERCICE DE MATHS 15
| A = ( 3Χ - 4 )( -6 + Χ ) → a) Χ = -2 | A = ( 3Χ - 4 )( -6 + Χ ) → b) Χ = 7 |
| A = [ 3 × ( -2 ) - 4 ][ -6 + ( -2 )] | A = ( 3 × 7 - 4 )( -6 + 7 ) |
| A = ( -6 - 4 )( -6 - 2 ) | A = ( 21 - 4 )( -6 + 7 ) |
| A = ( -10 )( -8 ) | A = ( 17 )( 1 ) |
| A = 80 | A = 17 |
| A = ( 3Χ - 4 )( -6 + Χ ) → c) Χ = -1,5 | A = ( 3Χ - 4 )( -6 + Χ ) → d) Χ = -11 |
| A = [ 3 × ( -1,5 ) - 4 ][ -6 + ( -1,5 )] | A = [ 3 × ( -11 ) - 4 ][ -6 + ( -11 )] |
| A = ( -4,5 - 4 )( -6 - 1,5 ) | A = ( -33 - 4 )( -6 - 11 ) |
| A = ( -8,5 )( -7,5 ) | A = ( -37 )( -17 ) |
| A = 63,75 | A = 629 |
| EXERCICE DE MATHS 16 | Nombres relatifs en écriture décimale |
|
a et b et c trois nombres relatifs en écriture décimaux |
| Sachant que : a + b = -15 et a + c = 102 et b + c = 63 |
| 1 - calculer : ( a + b ) × ( a + c ) - ( b + c ) |
| 2 - calculer : b et c tel que a = 12 |
CORRECTION EXERCICE DE MATHS 16
| 1 - calculer : ( a + b ) × ( a + c ) - ( b + c ) | |
| = ( a + b ) × ( a + c ) - ( b + c ) | |
| = -15 × 102 - 63 | |
| = -1530 - 63 | |
| = -1593 | |
| 2 - calculer : c | calculer : b |
| On a a + c = 102 et a = 12 | On a a + b = -15 et a = 12 |
| a + c = 102 | a + b = -15 |
| c = 102 - a | b = -15 - a |
| c = 102 - 12 | b = -15 - 12 |
| c = 90 | b = -27 |
| FICHES DE MATHÉMATIQUES POUR LE NIVEAU QUATRIÈME |

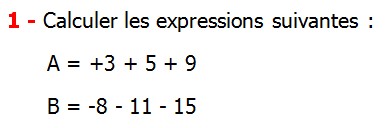


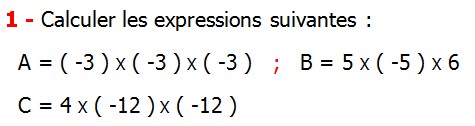

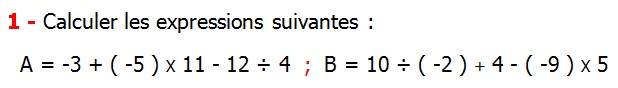
![Exercices corriges de Maths 4ème Nombres relatifs en écriture décimale Calculer l’expression suivante A = -24 + [ ( -14 ) X 2 + 12 ] ÷ [ 5 - ( -4 ) ÷ 4 ] X 3](http://www.lemathematique.com/uploads/articles/eefac7d5.jpg)